Introducción
Una forma de entender un modelo supervisado de Machine Learning, es analizando las partes que la componen. En específico, prácticamente todos los modelos supervisados se pueden dividir en 4 componentes: Data, Modelo, Función de perdida y Algoritmo de optimización. Los cuales (procurando mantener la consistencia entre ellas) nos otorgan una gran flexibilidad para construir modelos que se adapten de mejor forma al contexto y objetivos del problema en cuestión (ver: Deep Learning para más detalles). A continuación describimos cada componente, poniendo un mayor enfoque en un método específico de optimización: Gradiente Descendente.
Carga librerías, layout
# Importamos las librerías necesarias
import pandas as pd
import numpy as np
# Para generar datos aleatorios asociados a una regresión lineal bivariada
from sklearn.datasets.samples_generator import make_regression
#definimos como queremos mostrar los números en la tabla.
pd.options.display.float_format = '{:,.2f}'.formatData
Son los ejemplos con los que queremos que el modelo aprenda. Se caracterizan por disponer de variables independientes ($x$) y las etiquetas o variable dependiente ($y$).
Ejemplo:
# 100 obs, con 2 variables indep (ambas explicativas), 1 dep y 4 de desviación
# estandar (4). Fijamos random_state=0, para siempre obtener los mismos
# valores
X, y = make_regression(n_samples=100, n_features=2, n_informative=2,
random_state=0, noise=4)x1 = X[:,0]
x2 = X[:,1]df = pd.DataFrame({'x1': x1,
'x2': x2,
'y': y})
df = df[['x1', 'x2', 'y']]
df.head(10)| x1 | x2 | y | |
|---|---|---|---|
| 0 | 1.05 | -1.07 | -73.43 |
| 1 | -0.36 | -0.63 | -72.57 |
| 2 | -0.85 | 0.31 | 4.77 |
| 3 | 1.33 | 0.30 | 65.41 |
| 4 | -0.46 | -1.32 | -142.68 |
| 5 | 1.94 | -1.17 | -55.50 |
| 6 | -1.60 | 0.63 | 22.56 |
| 7 | -0.40 | 0.18 | 3.16 |
| 8 | -0.98 | 1.87 | 155.49 |
| 9 | 0.38 | 0.15 | 24.31 |
Modelo
Teniendo la data, ahora el siguiente desafío es establecer una estrategia de cómo intentar estimar la variable dependiente ($y$) a partir de solo las independientes ($x_1, x_2$). Representando esta tarea, el objetivo central de los modelos supervisados. Para lograr esto, necesariamente debemos transformar las variables independientes ($x_1, x_2$), para llegar a un estimación que tenga la misma forma que $y$. Para distinguir $y$ de nuestra estimación, a este última le llamaremos $\hat{y}$.
La pregunta siguiente es: Qué transformación utilizar? Y es una excelente y central pregunta. Pero, para poder responderla, debemos entender un par de conceptos que veremos en las siguientes secciones. Por lo que por ahora, dejémosla por un momento de lado y supongamos que ya disponemos de una transformación inicial la cual modificaremos más adelante. En específico supongamos que nuestra transformación es del tipo $f(x_1, x_2) = \beta_1x_1 + \beta_2x_2$. Donde como parámetros iniciales elegimos $\beta_1 = 2$ y $\beta_2= 1$ , es decir:
\[f_0(x_1, x_2) = 2x_1+ 1x_2 = \hat{y}\]Para evitar confusiones, se debe establecer que los indices de $x_1$ y $x_2$, corresponden al número de columna, no el de fila.
Que pasa si aplicamos esa transformación a nuestras datos?
df.loc[:,'y_gorro'] = 2*df['x1'] + 0*df['x2']
df.head(5) # solo mostramos las 5 primeras filas para no sobrecargar el display.| x1 | x2 | y | y_gorro | |
|---|---|---|---|---|
| 0 | 1.05 | -1.07 | -73.43 | 2.11 |
| 1 | -0.36 | -0.63 | -72.57 | -0.73 |
| 2 | -0.85 | 0.31 | 4.77 | -1.71 |
| 3 | 1.33 | 0.30 | 65.41 | 2.65 |
| 4 | -0.46 | -1.32 | -142.68 | -0.92 |
Ok. Vemos que generó estimaciones… Pero tienen un real uso?. Por ejemplo vemos que el modelo estimó, para la primera observación, en base solo a las variables independientes ($x$), que $\hat{y} = 2.11$, sin embargo el valor real $ y = -73.4$. Al parecer se equivoca, y bastante!
Para intentar lograr mejores estimaciones, lo primero es tener manera de cuantificar que tan lejos estamos de los valores reales. Esto se llama función de pérdida, y lo veremos en la sección que sigue.
Naturalmente, regresión lineal no es el único modelo posible. Más bien es solo uno de una gran cantidad de distintos tipos que podríamos haber propuesto. Ejemplos de esto son: Árbol de Decisión, Support Vector Machines, redes neuronales, etc. A modo de entendimiento informal, esta se diferencian principalmente en el espacio de hipótesis que tienen disponible para explorar y el tipo de variable dependiente con la que deseamos implementarlo. Por ejemplo, para el caso de regresión lineal, el espacio de hipótesis son todas las combinaciones de relaciones lineales del tipo $\beta*x$ que podemos construir. Distinto es el caso de árbol de decisión, donde estamos buscando combinaciones de reglas binarias a partir de las variables independientes. Estas breves descripciones, claramente no le hacen justicia a todos los detalles que comprende cada tipo de modelo, pero para efectos de este post lo dejaremos hasta aquí para concentrarnos de mayor forma en la función de pérdida y el método de optimización.
Nota: Una descripción más rigurosa es posible de encontrar en libros mencionados en posts anteriores cómo Machine Learning de K. Murphy o The Elements of Statistical Learning.
Función de pérdida
Informalmente, la función de perdida corresponde a la forma en que cuantificamos la lejanía de cada una de nuestras estimaciones vs los valores reales. En el ejemplo anterior, a primera vista percibimos que estábamos bastante alejados de los valores reales, pero “a primera vista” no es suficiente, debemos ser más específicos. Idealmente nos gustaría, de forma automática y objetiva, una manera de cuantificar esta “lejanía”. Esto nos permitirá ampliar nuestra capacidad de poder probar múltiples modelos de manera eficiente.
Naturalmente la función de perdida, que llamaremos $L$, debe tomar como input tanto los valores reales como las estimaciones de nuestro modelo $\hat{y}$. De otra forma, como será capaz de comparar ambas? Tenemos que necesariamente relacionarlas. Por otro lado, también nos gustaría que posea ciertas propiedades en linea con nuestro objetivo. Algunas de estas propiedades se describen a continuación. Sin embargo estas carecen de una análisis matemático riguroso (por ejemplo, una propiedad importantísima que no se describe, es diferenciabilidad). Esta decisión fue intencional, para así mantener los conceptos del post en un plano accesible a una mayor audiencia:
-
Adecuado: Nos gustaría que la función entregue respuesta directa a las necesidades del problema. Por ejemplo, si no nos importa tanto que el modelo se equivoque con tal que no lo haga de gran forma, nuestra función debiese reflejar eso.
-
Consistente: Nuestra función debe representar consistentemente que tan lejos o cerca nuestras estimaciones están vs los valores reales. Por ejemplo, si tenemos 2 pares de valores-reales y predicciones, para las observaciones $A$ y $B$: $(y_A , \hat{y_A})$ y $(y_B, \hat{y_B})$. Si la lejanía real de $(y_A , \hat{y_A})$ es menor que la real de $(y_B , \hat{y_B})$, entonces $L(y_A , \hat{y_A})< (y_B , \hat{y_B})$.
-
Simple: A su vez, es deseable que nuestra función sea fácil de analizar para comprender de manera fácil los resultados obtenidos. Parece obvio no? Si… pero lamentablemente esto no siempre es posible. Teniendo muchas veces que sacrificar simplicidad en virtud de cumplir con las propiedades anteriores y diferenciabilidad. (Para un ejemplo de una función más compleja ver: You Only Look Once: Unified, Real-Time Object Detection)
En vista de lo anterior, postulemos un escenario que nos servirá para comprender más directamente el rol que cumple cada propiedad: Esto es, que para este problema nos importa penalizar en mayor medida las grandes desviaciones versus las desviaciones pequeñas. Ojo, que para otro problema, puede que este escenario no sea conveniente. Esto es perfectamente posible, solo supongan que para este si lo es.
Con esto, exploremos algunas funciones de perdidas, verificando si cumplen o no, con las propiedades que hemos planteado.
Suma de residuos:
\(L_1(y,\hat{y}) = \sum_{n=1}^{N}{y_i-\hat{y_i}}\)
residuos = (df['y']- df['y_gorro'])
pd.DataFrame(residuos, columns = ['Residuo']).head(9)| Residuo | |
|---|---|
| 0 | -75.54 |
| 1 | -71.84 |
| 2 | 6.48 |
| 3 | 62.76 |
| 4 | -141.75 |
| 5 | -59.38 |
| 6 | 25.76 |
| 7 | 3.96 |
| 8 | 157.45 |
L_1 =residuos.sum()
round(L_1, 2)355.66
Esta es quizás la función más simple que podemos proponer. Aquí es fácil ver que cumple la propiedad 3. Sin embargo, no cumple ninguna de las otras 2 propiedades:
Adecuado: Al inspeccionar la función vemos que cada unidad de desviación se considera de la misma forma. Que independiente que sean desviaciones mayores o menores en magnitud, aportan de igual manera.
Consistente: Viendo la tabla de residuos, notamos que todos estos son negativos. Pero que sucede si por ejemplo obtenemos un residuo muy pequeño y positivo? De acuerdo al criterio de nuestra estimación, sería menos “cercano” que cualquiera de las estimaciones presentadas en la tabla, cuando lo real es lo contrario.
Error absoluto medio:
\(L_2(y,\hat{y}) = \sum_{n=1}^{N}\frac{|{y_i-\hat{y_i}}|}{N}\)
residuos = abs(df['y']- df['y_gorro'])/len(df)
pd.DataFrame(residuos, columns = ['Residuo']).head(5)| Residuo | |
|---|---|
| 0 | 0.76 |
| 1 | 0.72 |
| 2 | 0.06 |
| 3 | 0.63 |
| 4 | 1.42 |
L_2 = residuos.sum()
round(L_2, 2)83.04
Adecuado: La modificación planteada no nos ayuda en este sentido. Las unidades del residuo siguen siendo consideradas de igual forma, independiente de si corresponden a una desviación mayor o no.
Consistencia: Al tomar los valores absolutos, nos aseguramos que siempre compararemos en términos de magnitudes. Ahora, los residuos si representan el grado de “lejanía”, que vemos en $y_i$ vs $\hat{y_i}$
Raíz de Error cuadrático medio:
\(L_3(y,\hat{y})=\sqrt{\sum_{n=1}^{N}\frac{({y_i- \hat{y_i}})^2}{N}}\)
residuos = np.square(df['y']- df['y_gorro'])
pd.DataFrame(residuos, columns = ['Residuo']).head(5)| Residuo | |
|---|---|
| 0 | 5,706.14 |
| 1 | 5,161.18 |
| 2 | 41.97 |
| 3 | 3,938.64 |
| 4 | 20,094.05 |
L_3 = np.sqrt(residuos.sum()/len(df))
round(L_3, 2)101.99
Adecuado: Al elevar al cuadrado cada residuo. Logramos justamente lo que queremos, penalizar las observaciones donde la magnitud del residuo es mayor.
Consistencia: Otra propiedad de la función cuadrática es que su resultado siempre es $> 0$ para los números reales. Así, independiente de si nuestra estimación es mayor o menor en comparación con el valor real, siempre los podremos comparar consistentemente.
Nota: Las 2 últimas métricas son sólo un subconjunto de una amplia gama de funciones de pérdida comúnmente disponibles (incluso podemos crear nuestras propias funciones). Para una descripción más exhaustiva y completa de ellas, sugerimos revisar los libros anteriormente mencionados
Algoritmo de Optimización:
Al haber elegido la función que nos cuantifica el error de nuestras estimaciones frente a los valores reales, solo nos queda un último ingrediente para construir nuestro modelo: El algoritmo de optimización.
En palabras sencillas, dada nuestra función de perdida, sabemos que mientras menor sea el error total, mayor será la cercanía entre nuestras estimaciones y los valores reales. Así, como en nuestro caso estamos tratando de ajustar un modelo del tipo lineal $\beta*x$, solo podemos manipular los elementos que nosotros controlamos, en este los $\beta$, pará así minimizar este error. En matemáticas, las herramientas que buscan ya sea encontrar el mínimo o máximo, de una función se llaman algoritmos de optimización. En este caso el mínimo simplemente lo escribiremos como $min(L(\beta_1, \beta_2))$
A pesar que en la literatura podemos encontrar una gran cantidad de algoritmos que nos permiten realizar esto, uno de los más populares, sin lugar a dudas es gradiente descendente. El cual es ampliamente usado en redes neuronales y es el foco de este post.
Antes de entrar a revisar las ecuaciones, me gustaría plantear la siguiente historia para explicarlo en términos más intuitivos:
Pedro tiene unos viejos amigos, los cuales disfrutan haciéndole regalos elaborados para cada cumpleaños. En esta ocasión, para su cumpleaños número 40, quisieron que fuese uno que superara a todos los anteriores. Ahorraron mucho dinero y tuvieron el maravilloso plan de secuestrarlo, vendándole los ojos y luego tomando un helicóptero, para dejar a Pedro perdido entremedio de la montaña. (Lo acepto, es un tanto raro el ejemplo, pero créanme, les ayudará a entender el algoritmo más rápidamente)
Al dejarlo ahí sus amigos – además de entregarle un altímetro que mediante sonido le indica su altura actual – le dicen que a los pies de la montaña ($altura = 0$) esta su verdadero regalo y todo lo que tiene que hacer es llegar hasta ahí para cobrarlo. El mayor problema eso sí, es que la venda fue especialmente diseñada para quién la usa no se la puede sacar. La pregunta entonces es evidente:
¿Que tendría que hacer Pedro para llegar a los pies de la montaña? Ante eso, la solución que se plantea es bastante simple. Es tratar de percibir, mediante la pisada, la inclinación del suelo, dando un paso hacia la dirección de mayor descenso… Perfecto!, pero ahora la pregunta siguiente es ¿Que tan largo debiese ser ese paso?
Si Pedro se siente con suerte, dará largos pasos, confiando en que recorrerá mayor terreno y llegará más pronto a la meta. Sin embargo, con esta estrategia Pedro corre un riesgo, ¿Que pasa si entremedio de ese paso la inclinación del suelo, deja de descender y sube nuevamente? Pedro, incluso podría llegar a un punto aún más lejano del que estaba hace un paso atrás.
Otra estrategia, es dar pasos muy pequeños recorriendo muy minuciosamente el terreno. El problema con esta estrategia es obvia, probablemente se demore demasiado y no llegue nunca a cobrar su regalo. La respuesta final, del largo del paso a dar, la detallaremos en la siguiente sección. Por ahora, recordemos nuestros datos, modelo y función de perdida, viendo como cada una de ellos contribuyen para el algoritmo.
En este sentido, nuestro modelo inicial $f_0(x_1, x_2)= \beta_1x_1 + \beta_2x_2 = 2x_1+ 1x_2$, vendría siendo lo mismo que la posición inicial de Pedro. Mientras que $f_{final}(x_1, x_2) = \beta_1^{final}{x_1} + \beta_2^{final}{x_2}$, vendría siendo la posición final o los pies de la montaña, que minimiza la función de perdida. Continuando con la analogía entonces, los pasos que daremos para llegar desde esa posición inicial hasta la final, es mediante gradiente descendente. Finalmente, la función de perdida, correspondería al altímetro de la historia, indicándole a Pedro la diferencia de su posición con respecto a los pies de la montaña o altura cero.
Para mayor claridad presentamos el siguiente seudocodigo, que traduce todo lo mencionado en el párrafo anterior:
modelo_i = f_0 #inicializamos con nuestro primer modelo
for i in range(max_iters): #Iteramos una cantidad arbitraria de veces.
# en este caso max_iters.
y_gorro = modelo_i(x) #definimos nuestras estimación
error = L(y, y_gorro)# y función de perdida
if error <= min_perdida: #Verificamos si nuestro algoritmo
# convergió a un mínimo de perdida,
# para detenernos antes.
break #end loop
else: #mientras no lleguemos al mínimo
modelo_i = actualizar(modelo_i) #actualizamos nuestro modelo
modelo_final = modelo_i #nos quedamos con el modelo final
error_final = error # y con nuestro error de ese modelo
Revisemos las lineas más importantes del código anterior:
Antes del loop de iteración, lo único que hacemos es establecer el criterio
mínimo de perdida (min_perdida) y la inicialización de nuestro primer modelo
(f_0). El criterio mínimo de perdida, es una suerte de criterio de
convergencia. Indicándole al algoritmo en que momento nuestro estaremos
satisfechos con el error obtenido para que este se detenga.
Luego empieza nuestro for loop de iteración. Para que no itere eternamente se
debe establecer un número razonable. Dentro de este loop, primero calculamos
nuestras estimaciones (y_gorro) para y, a partir de las variables
independientes (x). Al tener nuestras estimaciones, simplemente las
utilizamos, en conjunto con los y reales para calcular el error. Finalmente,
verificamos si el modelo convergió (condición if) o no (condición else).
Dentro de la segunda condición, lo primero que hacemos es actualizar nuestro
modelo mediante la función actualizar(). Sin este paso, es como si Pedro
después que lo haya dejado el helicóptero, se quedara inmóvil. Para llegar a los
pies de la montaña, necesariamente debe modificar su estado actual. Lo mismo
para nuestro algoritmo, para intentar superar el criterio de convergencia o
reducir el error, necesitamos actualizar nuestro modelo. Los detalles de como
funciona actualizar(), los veremos enseguida.
Una vez finalizado el for loop, ya tenemos nuestro modelo_final y
error_final. Los cuáles los podemos usar para realizar estimaciones de $y$, a
partir de solo las variables independientes ($x_1, x_2$). Debemos mencionar, que
no necesariamente error_final será 0. Puede ser > min_perdida incluso. Esto
dependerá, en conjunto, de la combinación de la data disponible, el tipo de
modelo elegido, el número de iteraciones y cómo actualizamos nuestro modelo
(gradiente descendente).
Función de actualización
De acuerdo al seudo código, la función de perdida ($L$) necesita dos parámetros:
y e y_gorro. El parámetro y es bastante fácil, es la variable dependiente
obtenida directamente de nuestra data. y_gorro en cambio es nuestra estimación
a partir de la aplicación de distintos $\beta$ para cada variable independiente
(x1 y x2). Para calcular $L$ a pesar que notamos que depende de 5
componentes: y, x1, x2, $\beta_1$ y $\beta_2$, los únicos que controlamos
y que en verdad son variables a ojos de gradiente descendente son $\beta_1$ y
$\beta_2$, el resto siempre permanece constante. Así – como en los problemas de
optimización se trata de encontrar las variables que minimizan (o maximizan) una
función– nuestro problema entonces se resume en encontrar, mediante gradiente
descendente, los $\beta_1$ y $\beta_2$, que minimizan $L$, o más formalmente:
$\arg\min_{\beta_1, \beta_2}L(\beta_1, \beta_2)$.
Recordando la historia de Pedro, su estrategia es básica era: A partir de una
posición inicial, descender 1 paso a la vez hacia la dirección de mayor descenso
hasta llegar a los pies de la montaña. La acción de tomar ese paso es el
verdadero motor de nuestro algoritmos y a lo que en nuestro caso le denominamos
actualizar(). La cual, cómo su nombre lo indica, utiliza de forma directa el
cálculo de la Gradiente
(${\nabla}L(\beta_1, \beta_2$).
Esta operación, dada su importancia, merece un pequeño recordatorio. La cual será especialmente útil para los lectores que no recuerdan sus clases de Cálculo. En esencia, la gradiente se obtiene por medio del calculo de las derivadas parciales para cada variable de la función, la cual como vector nos entrega la dirección de mayor ascenso de una función diferenciable (ver figura). Como en nuestro caso estamos buscando el mínimo y no el máximo, simplemente debemos multiplicarla por -1, lo que la convierte en la dirección de mayor descenso. Nuestro algoritmo entonces en cada punto calcula la gradiente de la función de perdida y luego da un paso en esa dirección, hasta llegar (esperemos) hasta el mínimo. Cabe decir, que en cada punto nuevamente debemos calcular la gradiente, porque estas, al igual que nuestra función de perdida, dependen de $\beta_1 y \beta_2$, las cuales van cambiando en cada paso que tomamos.
Cómo paréntesis, en caso que no te acuerdes de dónde salen las derivadas parciales, la siguiente imagen muestra un ejemplo. Acá tomamos una función $L(\beta_1, \beta_2)$, y luego calculamos la derivada de ella vs $\beta_1$ considerando $\beta_2$ como constante. Esto mismo, lo repetimos con $\beta_2$ para completar la gradiente.
%matplotlib notebook
from IPython.display import Image
Image("derivada_parcial.png")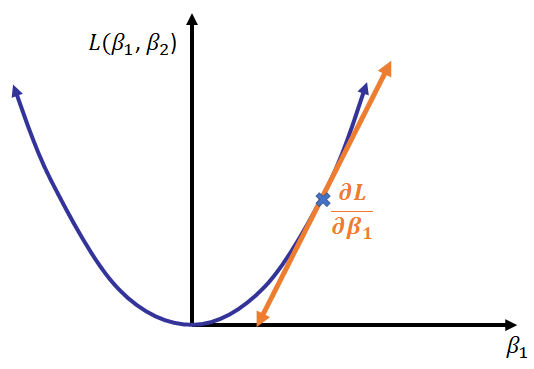
El último ingrediente que nos queda para generar la función actualizar(), es
fijar de que tamaño debe ser el paso. Este termino en gradiente descendente
recibe el nombre de learning rate (lr) o ratio de aprendizaje. Y determina que
tan rápido queremos avanzar hacia el mínimo. Como dije anteriormente, debemos
ser cuidadosos de que valor elegimos. Si es muy pequeño, nuestro algoritmo se
demorará demasiado en converger al mínimo, y si es demasiado grande, incluso
diverger. El valor óptimo generalmente se obtiene con validación
cruzada, tema para otro
post.
Definamos primero las funciones que hacen el trabajo duro y que utilizaremos luego en nuestro algoritmo.
# Para calcular nuestra estimación de y a partir de "x1", "x2" y nuestro modelo
# definido por (b1, b2)
def get_y_gorro(b1, b2, x1, x2):
y_gorro = b1*x1 + b2*x2
return y_gorro# calcula el la raíz del error cuadrático medio a partir de los valores
# reales "y" y nuestras estimaciones "y_gorro"
def recm(y, y_gorro):
residuos = np.square(y- y_gorro)
return np.sqrt(np.sum(residuos)/len(residuos))Gradiente
La función de gradiente descendente merece al menos indicar la formula matemática.
Recordando $L(y , \hat{y})$:
\[L(y , \hat{y}) = \sqrt{\sum_{n=1}^{N}\frac{({y_i- \hat{y_i}})^2}{N}}\]El cual se puede reescribir como
\[L(y , \hat{y}) = \sqrt{\sum_{n=1}^{N}\frac{({y_i- (\beta_1x_1 + \beta_2x_2)})^2}{N}}\]La derivada parcial para $\beta_1$ entonces es:
\[\frac{\partial L}{\partial \beta_1} = {\sum_{n=1}^{N}\frac{-x_1({y_i- (\beta_1x_1+\beta_2x_2)})}{N}} = {\sum_{n=1}^{N}\frac{-x_1({y_i- \hat{y_i}})}{N}}\]def grad(y, y_gorro, x):
return (1/len(x))*np.sum((y- y_gorro)*-x)def gd(x1, x2, y, lr = 0.01, iters=1000, min_perdida = 0.4):
b1 = 2 # utilizamos los mismos betas iniciales antes propuestos
b2 = 1
betas = np.array([[b1, b2]]) # almacenamos en un arreglo para futuro uso
y_gorro = get_y_gorro(b1, b2, x1, x2) # calculo de nuestras estimaciones
error = recm(y, y_gorro) # calculo de error
errores = np.array([error]) # almacenamos en un arreglo para futuro uso
for i in np.arange(iters):
y_gorro = get_y_gorro(b1, b2, x1, x2) #estimaciones
error = recm(y, y_gorro) #error
errores = np.append(errores , error)
if error <= min_perdida: # condición de convergencia anticipada
break
else:
# Acá es donde actualizamos nuestro modelo
# cambiando cada beta de forma separada
b1 = b1 - lr*grad(y, y_gorro, x1)
b2 = b2 - lr*grad(y, y_gorro, x2)
betas = np.concatenate((betas, [[b1, b2]]), axis = 0)
return betas, erroresbetas_gd, errores_gd = gd(x1, x2, y, lr = 0.1, iters=100, min_perdida = 0.6)print('Beta 1:', round(betas_gd[-1, 0],2))
print('Beta 2:', round(betas_gd[-1, 1],2))
print('Error final:', round(errores_gd[-1],2))Beta 1: 28.97
Beta 2: 96.63
Error final: 3.78
Luego de una rápido loop, finalmente tenemos nuestros resultados.
Inspeccionándolos vemos que son bastante diferentes a nuestros $\beta$
iniciales. El ajuste (Error Final) es por otro lado bien parecido al ruido que
fijamos cuando creamos los datos aleatorios de muestra.
Como el código puede ser insuficientemente ilustrativo, proporcionamos un video utilizando los mismos parámetros, data y modelos utilizados en este post. Acá mostramos 3 gráficas. En la primera se visualiza una superficie en forma de bowl que viene a ser la función de perdida en función de $\beta_1$ y $\beta_2$. A su vez también se muestra una animación de como vamos actualizando $\beta_1$ y $\beta_2$, hasta encontrar el mínimo de la función, por medio de gradiente descendente.
Las otras dos visualizaciones son la misma representación gráfica de los datos (puntos) versus nuestro modelo (plano), pero vistas en distinto angulo. Acá se muestra como el plano va cambiando hasta tener el mayor ajuste posible versus los datos reales. Cómo el código que generó esas visualizaciones es un tanto engorroso y se distancia del objetivo central, no se incluye en este post. Los más interesados pueden visitar mi repositorio Github para revisarlo.
Lo importante de estas gráficas es que vemos cómo, a partir de un modelo prácticamente inútil, podemos converger a un modelo con un mínimo de error dada la data, modificando el modelo paso a paso. A pesar de lo simple de nuestro ejemplo, no debemos subestimar lo poderoso del método. Todos los algoritmos que conozco de Deep learning, por ejemplo, tienen como motor gradiente descendente. Las cuales utilizan los mismos conceptos aquí descritos, con algunas modificaciones varias (pero importantes!) como momentum, minibatch y back propagation. Estos algoritmos son los que han logrado resultados estado del arte en áreas cómo reconocimiento de voz y clasificación de imágenes, y han empujado la revolución en inteligencia artificial que estamos viendo hoy.
<video width="800" height="400" controls>
<source src="assets/videos/gradiente_descendente.mp4" type="video/mp4">
</video>