Esta es la segunda parte del post de preprocesamiento/entendimiento. Para contextualizarlo, recomendamos leer el post anterior. En este post nos enfocaremos en entendimiento. El código y los conceptos mostrados, están pensados para una audiencia de nivel introductorio.
Por conveniencia y claridad, mostramos solo el código referido a la etapa de entendimiento. Si se desean reproducir los resultados mostrados en sus propios computadores, sugiero incluir el código del post anterior.
Entender la Data
Cargamos nuevamente las librerías:
import numpy as np # para operaciones númericas/matrices
import pandas as pd # para tablas de datos
#import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
pd.options.display.float_format = '{:,.2f}'.format
import os #para funcionalidades relacionadas al sistema operativo (carpetas)%store -r autos_df
%store -r cols_numDetengámonos por un momento para plantear algunas hipótesis en torno al problema. Todas las hipótesis que plantearemos girarán al problema principal que hemos planteado para este dataset, cuales atributos son los contribuyen a un mayor precio de un vehículo? Este proceso además nos permitirá familiarizarnos con la data. Evaluando, entre otras cosas, que problemas subyacentes puede tener o otros datos sería interesante por recolectar.
Ahora, este es solo uno de los problemas posibles. Para un mismo dataset siempre podemos plantear más de un problema a abordar. Esto también, es parte del encanto de esta disciplina. Siempre podemos crear desafíos por resolver:
- Recordemos un poco cuales son las variables en que hemos querido enfocarnos:
(
horsepower,num_puertas,width,length,num_cilindros,engine_size,peak_rpm,body_style) y analicemos cada una de forma separada:horsepower: Es el poder máximo del motor. Mientras mayor esta métrica, más capacidad de aceleración tendrá el vehículo. Así, debemos suponer que este es un elemento deseable para los consumidores, por lo que esperamos un mayor precio a medida que este aumente.num_puertas: Acá es un poco más difuso. Los convertibles por lo general tienen 2 puertas, por lo que si suponemos que todos los vehículos de dos puertas son convertibles, veríamos una relación negativa de numero de puertas vs precio. Sin embargo, hay autos de 2 puertas que no tienen tan alto precio. Por ejemplo, los city_cars. Probablemente así, esperaremos no ver una relación muy fuerte entrenum_puertasyprice.width,length: Los camiones y SUV, son autos de mayor tamaño y por lo general, más costosos. Sin embargo, no siempre se da que los vehículos de mayor tamaño, sean más costosos. Un contraejemplo, también resultan ser los convertibles.num_cilindros: La cilindrada $(C)$ viene a ser una suerte de capacidad pulmonar de los vehículos. Dónde a mayor cilindrada, mayor capacidad del vehículo, (y probablemente mayor precio). La cilindrada se calcula con $C = V*N$. Con $V$, volumen del cilindro y $N$ número de cilindros. Viendo tal ecuación, vemos que no siempre los autos que tengan mayor $N$ onum_cilindros, tengan mayor cilindrada. Así, puede suceder, que los cilindros de cada vehículo, tengan distinto volumen.engine_size: Esto es justamente la cilindrada. Por lo que esperamos un relación más estrecha (y positiva) entre esta métrica y el precio vsnum_cilindros.peak_rpm: Acá, de seguro los lectores detectarán que no soy experto en autos (corríjanme por favor en los comentarios si mi entendimiento es errado). Pero a grandes rasgos nos habla del nivel de rpm, donde el motor funciona a máximo poder. Así, como rpm, está relacionada con la aceleración del vehículo, a mayorpeak_rpmtendremos un mayor capacidad de obtener un buen poder y aceleración al mismo tiempo, lo cual es deseable para el comprador. Esto, sin embargo, no siempre es así. Por ejemplo, puede suceder que ese peak solo sea alcanzado en un rango muy estrecho de rpm, por lo que alcanzar este máximo de desempeño sea muy difícil de alcanzar. (referencia)body_style: Se refiere al tipo de chasis. Esperamos que para esta métrica, los automóbiles del tipo convertible (convertible,hardtop) tengan mayor precio que los otros.
Métricas de tendencia central:
autos_df[cols_num].describe()| price | horsepower | num_puertas | length | width | num_cilindros | engine_size | peak_rpm | |
|---|---|---|---|---|---|---|---|---|
| count | 197.00 | 197.00 | 197.00 | 197.00 | 197.00 | 197.00 | 197.00 | 197.00 |
| mean | 13,279.64 | 103.60 | 3.14 | 174.22 | 65.89 | 4.37 | 126.99 | 5,118.02 |
| std | 8,010.33 | 37.64 | 0.99 | 12.37 | 2.12 | 1.07 | 41.91 | 481.04 |
| min | 5,118.00 | 48.00 | 2.00 | 141.10 | 60.30 | 2.00 | 61.00 | 4,150.00 |
| 25% | 7,775.00 | 70.00 | 2.00 | 166.80 | 64.10 | 4.00 | 97.00 | 4,800.00 |
| 50% | 10,345.00 | 95.00 | 4.00 | 173.20 | 65.50 | 4.00 | 119.00 | 5,200.00 |
| 75% | 16,503.00 | 116.00 | 4.00 | 183.50 | 66.90 | 4.00 | 145.00 | 5,500.00 |
| max | 45,400.00 | 262.00 | 4.00 | 208.10 | 72.00 | 12.00 | 326.00 | 6,600.00 |
Con la anterior línea podemos devolver un resumen general de las principales
métricas de cada variable.
Viendo price vemos que su media está más cargada hacia valores bajos, donde el
75% de las observaciones bajo $45,400. Algo parecido sucede con horsepower,
donde el 75% de las observaciones bajo 116. Las variables length y width, al
parecer se comportan de una forma más parecida a una normal.
Correlación de Pearson:
autos_df[cols_num].corr().loc['price', cols_num[1:]]horsepower 0.81
num_puertas 0.05
length 0.69
width 0.75
num_cilindros 0.71
engine_size 0.87
peak_rpm -0.10
Name: price, dtype: float64
La linea anterior nos muestra la correlación de Pearson de todas la variables
cols_num vs price. Para destacar, es que a través de esta métrica, medimos
el grado de relación lineal entre cada variable y precio. Que una correlación
sea 0, no necesariamente significa que esta variable no tenga relación con el
precio. Solo que esta relación, si es que existe, es no lineal.
Aún así, vemos que las variables horsepower, length, width, horsepower,
engine_size y num_cilindros, presentan una alta correlación con price. El
paso siguiente, es si visualmente estas relaciones son evidentes…
Visualización
from pandas.plotting import scatter_matrix
scatter_matrix(autos_df[cols_num], figsize=(10, 10));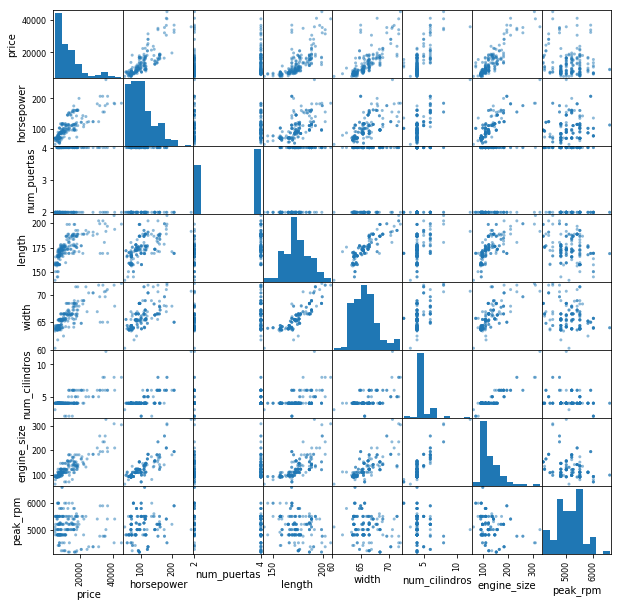
La primera línea de la celda anterior, es una simple importación de la función de matriz de dispersión. Los gráficos de dispersión son ampliamente usados cuando las variables en cuestión son cuantitativas. Permiten teorizar de buena forma, como se relaciona una variable versus la otra.
Mientras que en la segunda, aplicamos tal función. El resultado de esta es una matriz donde todas los cuadros, salvo los de la diagonal, son gráficos de dispersión. Para la diagonal en cambio, para no mostrar un gráfico de dispersión redundante, se muestra un histograma,la cual representa de forma aproximada la distribución de cada variable.
Fijándonos solo en la primera fila, (la que tiene como eje y precio) vemos
cosas interesantes. A la vez que engine_size, width y num_cilindros,
muestran una relación marcadamente
lineal el relación a price, variables
como horsepower o length, muestran una tendencia a una relación más bien
cuadrática. Este
hallazgo entonces, nos abre una nueva puerta. ¿Que tal si en vez de mirar una
relación del tipo $y = x$, transformamos x para que investigar $y = x^2$ ?. Es
una pregunta interesante que quizás vale la pena mirar, al igual que otras que
puedan surgir.
Ante eso, hay que entender que la generación de nuevas hipótesis es un proceso constante y que solo termina cuando nosotros así lo definamos. En la práctica, el analista siempre deberá estimar si el tiempo a invertir en investigar estas hipótesis tiene el potencial para adquirir conocimiento valioso para el problema o no. Como en todo proceso de este tipo, siempre este trade-off estará presente.
ax = autos_df[['price', 'body_style']].boxplot( by = 'body_style')
ax.set_title("")
ax.get_figure().suptitle("Price vs Body_style")
_= ax.set_ylabel('Price')
_= ax.set_xlabel('Body Style')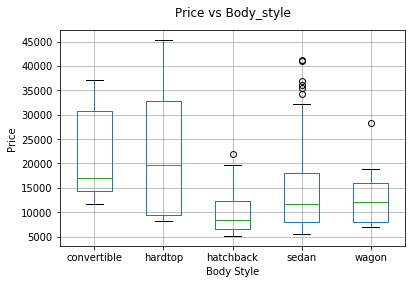
ax = autos_df[['price', 'num_puertas']].boxplot( by = 'num_puertas')
ax.set_title("")
ax.get_figure().suptitle("Price vs Numéro de puertas")
_ = ax.set_ylabel('Price')
_= ax.set_xlabel('Número de puertas')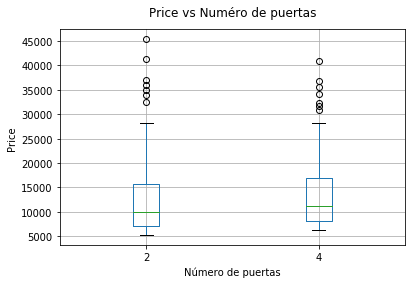
Como análisis final, se utilizan un tipo de gráficos que tienen quizás, el mejor
nombre de todos: Caja y Bigotes. Este tipo de gráficos es especialmente útil
para una entender la relación de una variable cualitativa u ordinal, versus una
cuantitativa. De modo muy breve, cada caja muestra la distribución de la
variable y versus un valor o categoría de la variable x. La linea inferior
de la caja marca el 25% de los datos, la linea verde el 50% y la linea superior
de la caja, el 75%. Las lineas horizontales de los bigotes marcan el mínimo y
máximo, sin considerar los outliers que se representan por pequeños círculos o
puntos.
Considerando lo anterior, en el primer gráfico vemos una clara tendencia a que
los vehículos del tipo convertible o hardtop, tengan un mayor precio,
mientras que los otros 3 tipos de chasis presentan un menor precio, sin haber
tanta diferencia entre uno y otro. Mientras que para la categoría sedan
muestra una mayor variabilidad.
En cuanto al segundo gráfico, no se ve mayor efecto del precio en virtud del número de puertas.
Comentarios Finales
Aquí termina nuestra primera travesía introductoria por el preprocesamiento y entendimiento de datos. El resultado de esto es haber obtenido conocimiento frente a un dataset, del cual solo teníamos hipótesis que todavía no habían sido verificadas. Cómo habrán notado, el desarrollo de estas etapas no fue del todo exhaustiva. Hay pasos al cual no le asigné el tiempo debido (por ejemplo: datos erróneos y omitidos) y conceptos que se podrían haber ilustrado de mejor manera (one-hot encoding). Esto fue absolutamente intencional, mi deseo era mostrar de principio a fin, los pasos más importantes de este proceso de principio a fin. Estaré atento a dudas o comentarios que tengan para así ir enriqueciendo este post.