Introducción

Un sitio que siempre me gusta compartir con conocidos es kaggle.com. Cada vez que lo menciono, me sorprende que todavía hay un buen numero entusiastas o practicantes de Machine Learning que no lo conocen. Este sitio, lo conocí en mis tiempos de estudiante de Magíster, donde, en uno de los cursos, nos pidieron participar de una de las competencias publicadas. Naturalmente, me entusiasmé con la dinámica y seguí participando en otras competencias meses después de haber concluido el programa de Magíster. A pesar que cada vez participo en las competiciones más infrecuentemente, sigo visitando Kaggle periódicamente, donde especialmente visito la sección de entrevistas a ganadores del blog de Kaggle “No free Hunch” .

En una de esas tantas visitas, leí una entrevista que me llamó particularmente la atención :Rossman 3rd Place Winner. La razón, la mención de una técnica derivada de Deep Learning aplicado a problemas de Procesamiento de Lenguaje Natural (NLP): Embeddings, pero que en su caso, utilizado para otro tipo de problemas. Si nunca han escuchado este término, deberían. En breve, esta técnica, fue popularizada por Google en el 2103 con Word2Vec y marcó un antes y después en el desempeño de los modelos enfocados a NLP. En resumen, lo que proponía el blog de Rossman es una idea simple pero tremendamente poderosa. ¿Que tal si aplicamos Embeddings a otro tipo de variables? De eso trata este post. De un tour guiado en la construcción de Embeddings. Mi intención es describir cada paso con un buen nivel de detalle, para que posteriormente puedan adaptar esta técnica en sus propios scripts. Espero que les guste.

Consideraciones

Antes de empezar el paso a paso para generar Embeddings, hay algunos aspectos a tener en consideración:

La técnica de Embeddings va de la mano con ajustar una red neuronal a nuestra dataset. Por ello entonces, necesitaremos importar una librería ad-hoc para tal propósito. En este caso PyTorch. A su vez, como está demostrado que trabajar con un procesador del tipo GPU, agiliza el entrenamiento de redes neuronales, utilizaremos un servicio GPU gratuito ofrecido por Google: Google Colab. Para los que no lo conocen, se los recomiendo. A pesar de ser algo limitada, es una buena alternativa para experimentar y probar ideas con este tipo de modelos.
En este post usamos un par de librerías menos comunes. En específico, además de las más conocidas Pandas, Matplotlib, Numpy , Sklearn y Pytorch, utilizaremos adjustText y xgboost. La primera para optimizar el despliegue de los textos en la visualización de Matplotlib y la segunda para comparar el desempeño de nuestra red neuronal con un tipo de modelo que usualmente logra buenos resultados.

import pandas as pd
import numpy as np

from sklearn import preprocessing
from sklearn import model_selection
from sklearn.manifold import TSNE

%matplotlib inline
import matplotlib.pyplot as plt

import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import Dataset, DataLoader

from adjustText import adjust_text

import xgboost as xgb

Carga Datos y Preprocesamiento

Carga Datos

df = pd.read_csv('adult.csv', sep=";", index_col=None)

Preprocesamiento

Para este artículo, utilizaremos uno de mis datasets favoritos: “Adult.csv”, presente, como siempre en el repositorio de la UCI – Machine Learning. Este dataset lo elegí por su gran número de observaciones (casi 50 mil) y por incluir varias variables del tipo categóricas. Este dataset contiene datos faltante que están marcados con un ‘ ?’. Dónde, las filas que presentaban al menos 1 columna con dato faltante no se consideraron. Esto para enfocarnos de mayor forma al tema central de este artículo.

df.replace(to_replace=' ?', value= np.nan, inplace=True)

df.dropna(inplace=True)

El dataset cuenta con 15 columnas, (14 independientes y una dependiente: income). De las variables independientes hay 8 del tipo categóricas, siendo el resto continuas.

df.columns

Index(['age', 'workclass', 'fnlwgt', 'education', 'education-num',
       'marital-status', 'occupation', 'relationship', 'race', 'sex',
       'capital-gain', 'capital-loss', 'hours-per-week', 'native-country',
       'income'],
      dtype='object')

Convertimos la variable de interés: income a formato binario.

df.income = df.income.replace({' <=50K': 0, ' >50K': 1})

Especificamos sólo las variables del tipo categóricas y continuas que consideraremos en nuestro análisis. Es decir no consideramos education y fnlwgt. La primera, por ser una variable redundante con education-num y la segunda porque, dada su descripción, potencialmente no aportaría mayor información para lograr un mejor desempeño del modelo.

categ_cols = ['occupation', 'workclass', 'native-country', 'marital-status', 'race', 'relationship', 'sex'] 
contin_cols = ['age', 'capital-gain', 'education-num', 'hours-per-week', 'capital-loss']

N_CONT = len(contin_cols)
N_CONT

Recodificación columnas categóricas.

Para poder trabajar las variables del tipo categóricas en pytorch, primero recodificamos las cadenas de texto de cada columna a una etiqueta numérica.

def encode_column(df, col):
    """
    Función que mapea cada categoría en la columna col de un dataframe a una
    etiqueta númerica. Transformando en su sitio la columna y devolviendo
    una tupla que contiene las etiquetas originales y transformadas.
    Input:
    df = Pandas DataFrame
    col = Nombre de columna
    Output: Tupla de etiquetas originales y transformadas.
    """

    e = preprocessing.LabelEncoder() # instanciamos un modelo de sklearn para
    # etiquetar numericamente cada categoría.
    e = e.fit(df[col]) # Ajustamos a la data
    df[col] =e.transform(df[col]) # Recodificamos la columna del df con 
    # etiquetas númericas
    return e.classes_, e.transform(e.classes_)# tupla de categ originales y 
    # nuevas etiquetas

categ_cols_mapping = {col: encode_column(df, col) for col in categ_cols}

Procesamiento variables contínuas

Por otro lado las variables continuas se deben estandarizar. Esto ayudará posteriormente, en el entrenamiento de nuestra red neuronal. Para ello utilizamos el módulo StandardScaler de sklearn.

scaler = preprocessing.StandardScaler()
df[contin_cols] = scaler.fit_transform(df[contin_cols])

Dataframe final

Para finalizar con el preprocesamiento concatenaremos las variables continuas, las categóricas recodificadas con etiquetas numéricas y las variables categóricas recodificadas mediante one hot encoding. Esto último, no se considerará para el entrenamiento de la red neuronal con pytorch pero si lo utilizaremos al entrenar nuestro ensamblaje (XGBoostClassifier).

"""
Esto lo realizaremos mediante el metodo concat de pandas. En breve, concat 
concatena dataframes según el eje que definamos. Pyede ser 0, si queremos 
concatenar agregando filas, y 1, si queremos concatenar agregando columnas.

Los dataframes a concatenar se entregarn a la función mediante una lista.
En este caso son 3 dataframes. El primer dataframe contiene 
las variables continuas y categóricas (etiquetadas númericamente).
El segundo dataframe, una transformación de las variables categóricas al método
one-hot encoding. Y el tercer df con nuestra variable dependiente: 'income'
""" 

df = pd.concat([df[categ_cols + contin_cols], 
           pd.get_dummies(data = df[categ_cols], 
                          columns = categ_cols, 
                          drop_first = True, 
                          prefix_sep = '_onehot_'),
          df['income']], axis = 1)

Train vs testing

Como es usual en machine learning, procedemos con generar un dataset de entrenamiento y otro de validación o testing para evaluar nuestros modelos. Esto lo realizaremos mediante el método train_test_split de sklearn, donde dejaremos un 20% para testing.

# Nuestro df tiene como última columna la variable dependiente. Por ello el -1.
# Además notar el uso de una semilla seudo-aleatoria, con el propósito 
# de replicabilidad en resultados.
train_x, test_x, train_y, test_y = model_selection.train_test_split(df[df.columns[:-1]], 
                                                                    df[df.columns[-1]] , 
                                                                    test_size = 0.2,
                                                                    random_state = 43)

Preparación especial: Etiquetas (Red Neuronal) y One-hot Encoding (XGBoost)

De la forma en que lo hemos especificado, cada modelo necesitará estructuras distintas de datos como input. Mientras que la red neuronal espera recibir una columna por cada variable categórica, XGBoost espera recibir las categorías en formato one hot encoding. Es decir, para cada variable, alimentar con $n-1$ columnas binarias, donde $n$ es el número de categorías de la misma.

Descripción One-Hot Encoding

De forma breve, one-hot encoding nos dice que cada vez que en la fila $i$ de la variable categórica original, se encuentre la categoría $j$, se debe marcar en la columna binaria $j$ de esa variable con un 1 y en caso contrario con 0. Esto para $n-1$ de las $n$ categorías. La razón que sean $n-1$ columnas binarias y no $n$ es para evitar entregar al modelo variables redundantes. Esta redundancia radica en que si sabemos que la columna está representada solo por $n$ categorías, siempre podríamos determinar la columna $n$ como resultado de la codificación de las anteriores $n-1$ columnas. A continuación mostramos un ejemplo de one-hot encoding.

Ejemplo One-hot encoding

# Dataframe original de ejemplo. Vemos una columna (palabra) de tipo categorica.
df_ej = pd.DataFrame(['Perro', 'Gato', 'Mesa'], columns = ['Palabra'])
df_ej

	Palabra
0	Perro
1	Gato
2	Mesa

La cuál convertimos a one hot encoding mediantes get_dummies. En este caso, Mesa sería redundante, dado que podríamos determinarla viendo que todo el resto de columnas (en este caso Gato y Perro) son todas 0.

pd.get_dummies(df_ej)

	Palabra_Gato	Palabra_Mesa	Palabra_Perro
0	0	0	1
1	1	0	0
2	0	1	0

En nuestro caso particular, para implementar el tratamiento especial de las variables independientes de entrenamiento, primero generamos una lista con todas las columnas del tipo one-hot encoding.

onehot_cols = train_x.columns[train_x.columns.str.contains('onehot', regex=False)]

Dataset red neuronal

Para el primer caso de nuestra red neuronal, no consideraremos las columnas del tipo one-hot. Esto lo realizaremos utilizando la función drop de Pandas.

train_x_nn = train_x.drop(onehot_cols, axis = 1)
test_x_nn = test_x.drop(onehot_cols, axis = 1)

Luego, transformamos de arreglos numpy (obtenidos por medio de .values) a tensores de pytorch. Para el caso de las etiquetas, necesitamos cambiar la estructura de datos para que así esté de acuerdo con lo que espera nuestra red neuronal. Finalmente, convertimos el tipo de datos de estos últimos a float.

inputs = torch.from_numpy(train_x_nn.values)
labels = torch.from_numpy(train_y.values.reshape(-1,1)).float()

inputs_test = torch.from_numpy(test_x_nn.values)
labels_test = torch.from_numpy(test_y.values.reshape(-1,1)).float()

Dataset xgboost

Para el segundo caso (xgboost). Consideraremos solo las columnas del tipo one- hot, además de las columnas del tipo continuas.

train_x_onehot = train_x[onehot_cols.tolist() + contin_cols]
test_x_onehot = test_x[onehot_cols.tolist() +  contin_cols]

Data Loaders de Pytorch

Para nuestra red neuronal, hay un último detalle a implementar. Convertir el dataset a un objeto del tipo DataLoader. Lo que buscamos con esto es poder entrenar nuestro modelo con mini-batches y que el orden de los mini-batches sea consumido por el modelo de forma aleatoria en cada época. Esto agilizará el entrenamiento del modelo.

class myDataset(Dataset):
    """
    Para crear un objeto del tipo DataLoader, debemos convertir nuestros tensores
    a un objeto pytorch Dataset. Esto se logra creando una clase que hereda de
    pytorch dataset, donde se debe especificar 3 funciones: __init__ 
    (donde creamos los atributos de etiquetas (labels) y variables 
    independientes (X)), __len__  (donde devolvemos el tamaño de nuestro dataset)
    y __getitem__ (para indexar nuestro dataset, o, en otras palabras,
    obtener a demanda la observación i del dataset)
    """
  
  
    def __init__(self, x, labels):
        self.labels = labels
        self.X = x

    def __len__(self):
        return len(self.X)

    def __getitem__(self, index):
        X = self.X[index,:]
        y = self.labels[index]
        return X, y

El último paso antes de crear los objetos DataLoader, es fijar las semillas aleatorias y decirle a pytorch que implemente algoritmos determinísticos en su backend.

torch.manual_seed(43)
torch.cuda.manual_seed(43)
np.random.seed(43)
torch.backends.cudnn.deterministic=True

Para tanto los datos de entrenamiento como testing vamos a crear objetos de tipo DataLoader.

trainloader = DataLoader(myDataset(inputs, labels), # tensores convertidos
                         batch_size=500, # tamaño de cada batch
                         shuffle=True, # orden aleatorio por cada epóca
                         num_workers=2) # cuanto procesamiento en paralelo deseamos

testloader = DataLoader(myDataset(inputs_test, labels_test), 
                        batch_size=500,
                        shuffle=True, 
                        num_workers=2)

Redes Neuronales con Embeddings

Introducción a Embeddings

Antes de seguir con el nuestro tour paso a paso, les comparto una explicación breve (con algo de historia) para ayudar a entender que son los Embeddings…

Durante mucho tiempo el problema de traducción automática de texto era un problema donde las soluciones implementadas, dejaban mucho por desear. Todavía recuerdo, hace ya varios años, cuando era muy evidente cuando alguien había traducido un texto con el traductor de Google. Por lo general parecían traducciones un tanto robóticas o no entendiendo bien, el contexto de cada palabra. Esto, sin embargo, cambió para mejor. Y a pesa que es verdad que el Traductor de Google sigue cometiendo errores, el avance es bien notorio.

Aunque se desconocen cuáles fueron todos los desarrollos que Google implementó para lograr esta mejoría, hay un que popularmente se destaca como un importante factor: La publicación de este paper: Distributed Representations of Words and Phrases and their Compositionality de Mikolov et al.. Muy resumidamente, en este artículo, citado en más de 11 mil ocasiones, los autores proponen una nueva técnica para crear de forma eficiente una representación continua y vectorial de palabras, que es precisamente la técnica de Word Embeddings. ¿Porqué esta técnica es tan importante? La respuesta tiene que ver con la dimensionalidad y el valor que entrega una representación continua de una variable, aspectos que explico en las secciones que siguen.

Dimensionalidad

Popularmente, por lo menos hasta el año 2013, una buena parte de los modelos que tenía que ver con el procesamiento de texto utilizaban one-hot enconding para representar texto en un formato que los modelos pudiesen consumir. Como vimos anteriormente, esta es una técnica simple y rápida de implementar, pero tiene varias desventajas. Entre ellas, y a mi gusto la más importante: su alta dimensionalidad. La alta dimensionalidad, en palabras sencillas, ocasiona que los modelos, que dependen de encontrar similaridades o patrones, les sea mucho más difícil su trabajo. Esto porque en alta dimensionalidad, las observaciones tienden a ser todas lejanas, pareciéndose entre si y, en términos prácticos, impidiendo al modelo poder distinguirlas.

En el caso de one-hot encoding, esta técnica genera una alta dimensionalidad porque crea una variable (columna) nueva por cada categoría o clase que existe en nuestra variable original. Así, si por ejemplo tenemos un corpus de 1 millón de palabras e implementamos one hot encoding, tendremos 1 millón -1 de variables nuevas.

Representación Continua.

Otra forma en que los modelos no puedan detectar patrones, es que en la forma que expresamos cada observación no permita distinguir, con precisión, cuales observaciones son más similares. Para ello, es altamente preferente que la representación de cada palabra sea continua vs discreta. En el caso de representación discreta, la capacidad de encontrar patrones se vuelve mucho más compleja. Esto se muestra, en el Ejemplo One-hot encoding mostrado en la sección de preprocesamiento, donde cada observación es equidistante entre sí ([1, 0 ,0] vs [0, 1 ,0] vs [0, 0 ,1]), por la que el modelo no podrá distinguir cuales son más similares. En el caso de representación continua de variables categóricas, nuestra flexibilidad es mucho mayor, tenemos todo el espacio real ($\mathbb{R}$) de números para caracterizar cercanías. El único desafío es poder encontrar esas representaciones continuas.

Esto es lo que nos gustaría para cada variable categórica. Sin embargo, hasta el momento, hemos hablado de Word embeddigs. Es decir representaciones vectoriales continuas de palabras. Pero. si lo notan, el salto hacia categorías no es mayúsculo, simplemente debemos ver cada variable categórica como una palabra pero con usualmente mucha menor cardinalidad. La capacidad de poder trabajar variables categóricas con embeddings, nos permite utilizar redes neuronales para datasets del tipo tabulares. Algo que hace poco, se consideraba poco adecuado, pero que ahora, mostraremos que es posible e incluso conveniente.

Entrenamiento de embeddings

Para poder generar nuestros embeddings lo primero es establecer cuantas dimensiones queremos para cada variable categórica. Este no es un número que conocemos, pero existen técnicas para definirla. Una sofisticada, es estimar la cantidad de dimensiones por medio optimización de hiperparámetros. Esto es, iteramos distintos valores para cada embedding, hasta seleccionar los valores que minimicen nuestra función de pérdida, evaluada en nuestra dataset de validación. Sin embargo, por simplicidad, en este artículo utilizaremos otra técnica. Ocupar una regla usualmente utilizada de considerar cada dimensión cómo la mitad del número de categorías presente en cada variable, con un tope máximo de 50 dimensiones.

El segundo paso es justamente entrenar los embeddings, lo cual lo hacemos mediante el entrenamiento de una red neuronal que incluya una capa de embeddings. Para introducirlos en el tema, a pesar que existe una gran cantidad de buena literatura ya disponible para entender las diferentes arquitecturas y elementos de una red neuronal, igualmente en este artículo incluimos una brevisima introducción, para así intentar facilitar el entendimiento de las secciones venideras.

Red Neuronal

En términos sencillos, una red neuronal es una serie de capas (tensores) y operaciones vectoriales, qué, mediante muchos ejemplos etiquetados, nos permiten descubrir patrones en la data. Para crear una red neuronal, es necesario definir su arquitectura, es decir sus capas y las relaciones. Es por ello que el abanico de arquitecturas posibles de redes neuronales es solo limitado por nuestra imaginación y por algunos principios de aritmética de matrices. El objetivo perseguido en el diseño de una red neuronal es de minimizar el error del modelo, el cual debiese apuntar a resolver el problema planteado.

Entrenamiento de una red neuronal

Las redes neuronales están compuestos, en su forma más básica por perceptrones o neuronas artificiales. Por lo tanto, para entender como entrenar una red neuronal, veamos como se entrena un simple perceptrón. Para ello incluimos un diagrama de uno.

%matplotlib notebook
from IPython.display import Image
Image("perceptron.png")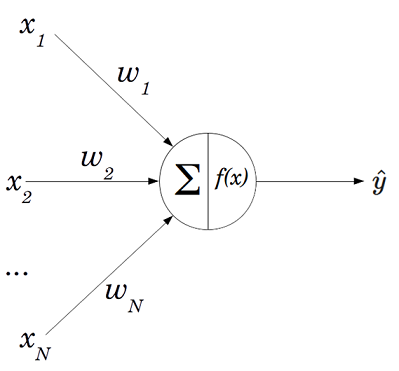

png

Las componentes más elementales del perceptrón, son los input ($x_i$), pesos ($w_i$), función de activación ($f(x)$), el output $\hat{y}$ y el error ($L$), el cual no se muestra en la figura. Para llegar desde los input hasta el output, primero se realiza una suma parametrizada de los input, $\sum^n_i w_ix_i$ (representado por $\sum$ en la figura). Para luego, pasar este resultado por la función de activación y generando el resultado $\hat{y}$.

El output – la estimación por parte del modelo de la variable dependiente – luego se compara con el valor real de la variable dependiente, donde (generalmente mediante gradiente descendente) se itera con el propósito de minimizar el error ($L$) entre las estimaciones y los valores reales.

Como paréntesis, a pesar, que en sus inicios tanto los input como el output del modelo se consideraron como variables binarias y se consideraba solo un perceptrón. Hoy en día la redes neuronales son de mucho mayor tamaño (concatenando una serie de perceptrones), con diseños bastante más flexibles, utilizando funciones de activación que no solamente devuelvan valores binarios y arquitecturas más complejas que no veremos en este articulo, como convolucionales y recurrentes.

A modo de entender como se entrena una red neuronal, describamos las componentes del perceptrón. En específico, detengámonos en un elemento que hasta el momento no hemos descrito con mayor detalle— los pesos $w_i$. Efectivamente, mientras que, por un lado, a partir de los datos podemos recolectar el input (variables independientes) y el output (variable dependiente) y, por otro, predefinimos una función de activación, los $w_i$ es un valor que no conocemos y que debemos descubrir. La manera en que encontramos tales valores, es instanciándolos con valores aleatorios, para luego, mediante gradiente descendente, iterar hasta encontrar los $w_i$ que minimicen el error entre $\hat{y}$ (las estimaciones del modelo ) e $y$ (los valores reales), encontrando, patrones en la data. Para el caso de embeddings, cada elemento de este cumple el rol de ser pesos ($w_i$) dentro de nuestra red neuronal.

La idea que de a partir de embeddings con valores aleatorios llegamos a una representación de las categorías que captura información y encuentra similitudes entre ellas, parece descabellada. Sin embargo, resulta. Y la manera cómo, es precisamente como una red neuronal aprende. Para ilustrar este proceso, tratemos de explicarlo mediante un ejemplo:

Supongamos que al inicio, tenemos dos observaciones con, respectivamente: $a$ y $b$ cómo valores de variables categóricas y con el mismo valor como variable dependiente ($y$), para cada observación. Siguiendo con la metodología de embeddings, cada categoría la representamos entonces como un vector continuo y aleatorio, es decir, las inicializamos totalmente disímiles entre sí. Una vez hecho esto, utilizamos estos embeddings de $a$ y $b$ (llamémoslos $E_a$ y $E_b$) , para estimar $\hat{y_a}$ e $\hat{y_b}$ respectivamente, los cuales, al utilizar vectores aleatorios, nos entregan estimaciones también aleatorias. Para este modelo, definamos que el error es del tipo $L = \sum^n_i \epsilon_i$, donde $i$, indexa cada observación, en nuestro caso entonces $L$ simplemente sería $\epsilon_a + \epsilon_b$. Luego de esto, supongamos también, para efectos de este ejemplo, que la suerte nos toca en que $\hat{y_a}$ resulta ser muy similar al valor real $y$, pero que $\hat{y_b}$ no – es decir, los valores para $E_a$, afortunadamente son óptimos, por lo tanto $\epsilon_a = 0$, pero $\epsilon_b \neq 0$, generado exclusivamente porqué $E_b$ no es óptimo.

Con estos elementos en pie, lo único que nos queda es definir que algoritmo de optimización utilizar para reducir $L$. Por lo general, para redes neuronales, se utiliza gradiente descendente, el cual fue explicado en un post anterior. Para no repetir, lo mencionado en aquel post, en resumen gradiente descendente poco a poco empezará a modificar los pesos $w$ (los embeddings en nuestro caso hasta encontrar los $w$ donde el error sea mínimo. En este caso, lo más probable es que gradiente descendente nos dirá que $E_b$ deberá ser muy similar a $E_a$, porque estamos suponiendo que en $E_a$, es donde el error se minimiza, $\epsilon_a = 0$. Esto es justamente el proceso mediante el cual encontrar similitudes en la data. Como sabemos que $\hat{y}_a = \hat{y}_b$, gradiente descendente nos dice que los pesos deben también ser similares. Entonces gradiente descendente modifica $E_b$ hasta llegar a eso. En muchas ocasiones eso si, tendremos muchas observaciones en conjunto con categóricas y continuas. En tales ocasiones, gradiente descendente deberá tomar en consideración todas las variables en conjunto con la variable dependiente, de cada observación, para calcular los embeddings, en pos de minimizar el modelo. A grandes rasgos es sí, el resultado para Embeddings es el mismo, Gradiente descendente nos entregará una representación continua de nuestras variables categóricas que minimiza el error considerando los patrones de la data. Aún más, estas nuevas representaciones optimizadas incluso las podemos utilizar para otros fines como veremos más adelante.

Modelo de embedding en Pytorch

Ya habiendo sentado las bases intuitivas del Embeddings, presentaremos un poco de código que nos ayudará a llevar estos conocimientos a la práctica. Para ello, el primer paso es crear una función que recorra cada columna y devolviendo un listado de tuplas con la cantidad de categorías y las dimensiones de cada embedding. En este caso, como lo habíamos mencionado anteriormente, dejamos la cantidad de dimensiones como la mitad del número de categorías. Esto se traduce en que creamos una lista de tuplas, donde cada elemento corresponde al número de categorías y de dimensiones del embedding por cada variable.

def get_embed_dims(df, categ_cols):
    return [(len(df[col].unique()), int(len(df[col].unique())/2)) for col in categ_cols]

embed_dims = get_embed_dims(df, categ_cols)

Ahora llegamos a la esencia de este post, donde definimos nuestro modelo de Pytorch utilizando el paquete nn. En concreto crearemos un modelo customizado, es decir, donde definiremos tanto las capas de nuestro modelo (función __init__) como las relaciones que deben existir entre ellas, (función forward), los cuáles se describen con mayor detención en los comentarios del modelo.

Otro punto es la estrategia para considerar variables categóricas y continuas en forma conjunta. Esto dado a que muy usualmente, nos encontraremos con datasets que incluyen variables categóricas y continuas cómo variables independientes, y es importante incluir ambas, si es que pensamos que pueden ser informativas para el modelo. En el caso de nuestro modelo, adoptaremos simplemente, una capa que concatena las representaciones continuas de las variables categóricas (Embeddings) y las variables continuas.

class EmbeddingModel(nn.Module):

    def __init__(self, n_cont, embed_dims, inter_dense, inter_dense_2, dropout = 0.1):
        """
        Función que permite crear una instancia de objeto Embedding Model
        Input:
        n_cont (int): Número de variables contínuas.
        embeds_dims (lista): Lista donde se epecifica (por categoría) el num de 
        categorías y de dimensiones de cada embedding.
        inter_dense (int): Tamaño del output de la primer capa de 
        transformación lineal.
        inter_dense2 (int): Tamaño del output de la segunda capa de 
        transformación lineal.
        dropout (float): Probabilidad que un elemento de input a esta capa sea 
        asignada con un 0. (Se utiliza como herramienta para prevenir el 
        sobreajuste del modelo).
        """
        # Llamamos al método __init__ del objeto padre de EmbeddingModel, es decir,
        # nn.Module
        super(EmbeddingModel, self).__init__()
        #almacenamos en la instancia la cantidad de variables contínuas.
        self.n_cont = n_cont
        self.embeds_list = nn.ModuleList([nn.Embedding(num_embeddings = vocab_size, 
                                     embedding_dim = e_dim) for vocab_size, e_dim in embed_dims])
        emb_sz = sum([e_dim for vocab_size, e_dim in embed_dims])
        self.linear1 = nn.Linear(emb_sz +n_cont, inter_dense)
        self.linear2 = nn.Linear(inter_dense, inter_dense_2)
        self.linear3 = nn.Linear(inter_dense_2, 1)
        self.dropout = nn.Dropout(dropout)

    def forward(self, inputs):
        """
        Para ilustrar como se relacionan las capas se incluye siguiente figura.
        Que muestra la capas desde el consumo de inputs (parte superior) hasta el
        output (parte inferior).
        """
        embeds = [emb(inputs[:, i].long()) for i, emb in enumerate(self.embeds_list)] 
        embeds = torch.cat(embeds, 1)
        embeds_cont = torch.cat(( embeds, inputs[:,-self.n_cont:].float() ), 1)
        embeds_cont = torch.relu(self.linear1(embeds_cont))
        out = self.dropout(embeds_cont)
        out = torch.relu(self.linear2(out))
        out = self.linear3(out)
        probs = torch.sigmoid(out)
        return probs

Embedding
model

Training

El siguiente paso es especificar como entrenaremos nuestro modelo.Para ello, primero instanciamos nuestro modelo (model) con los parámetros que se especifican. Luego, definimos el algoritmo para la minimización del error – en este caso Adam, que es una variante de Gradiente Descendente. Para, finalmente, especificar como calcularemos el error del modelo (BCELoss())

model = EmbeddingModel(n_cont = N_CONT, embed_dims= embed_dims,
                       inter_dense = 80, inter_dense_2 = 40, 
                       dropout = 0.17)
optimizer = optim.Adam(model.parameters())
loss_function = nn.BCELoss()

Ya con los objetos creados, entrenamos el modelo, donde los pasos principales se describen en los comentarios.

losses = [] # lista que almacena resultado de la función de perdida por época.
accs = [] # lista que almacenará los accuracies por época
data_size = len(trainloader.dataset) # tamaño del dataset de entrenamiento.

for epoch in range(100): #1 epoca = recorrer totalmente el dataset de 
    #entrenamiento
    correct = 0 # inicializamos el conteo de correctas y la perdida
    running_loss = 0.0
  
    for i, data in enumerate(trainloader, 0): # cada iteración es un batch 
        #de data
        inputs, labels = data # dividimos la data en vars indpts (inputs) y 
        # depdts (labels)
        optimizer.zero_grad() # setea todas las gradientes en 0 en backprop.

        outputs = model(inputs) # Generamos el output del modelo
        loss = loss_function(outputs, labels) # la perdida del modelo
        # versus las etiquetas reales.

        loss.backward() # calculamos las gradientes
        optimizer.step() # actualizamos los parametros del modelo

        # Métricas
        running_loss += loss.item() # recolectamos la pérdida de iter actual

        predicted = (outputs>0.5).float() # Las estimaciones del modelo según 
        # la codificación especificada anteriormente de income.
        truth = (labels>0.5).float() # las etiquetas reales
        correct += (predicted == truth).float().sum() # Cantidad de preds
        # correctas

  
    accs.append(correct/data_size)  # Accuracy de cada epoca
    losses.append(running_loss/data_size) # Perdida total de la época
print('Fin Entrenamiento')

Fin Entrenamiento

Mostramos los 5 últimos accuracy de entrenamiento.

accs[-5:]

[tensor(0.8667),
 tensor(0.8665),
 tensor(0.8684),
 tensor(0.8697),
 tensor(0.8673)]

Los más conocidos en el tema, sabrán, sin embargo, que el desempeño del modelo en la data de entrenamiento no es lo más relevante. Más bien que el que nos entrega una mejor estimación del error real de generalización es el desempeño en el dataset de testing. Calculémoslo!

Test Evaluation

data_size = len(testloader.dataset)

model.eval() #cambiamos a modo de evaluación
with torch.no_grad(): # comunicamos a pytorch que queremos desactivar el cálculo
  # automatico de gradientes. Lo que reduce memoria y agiliza el análisis.
  # El resto del script es parecido al código referente a entrenamiento
  # con la excepción que solo es 1 pasada por los datos.
    correct = 0 
    total_loss = 0
    for data in testloader:
        inputs, labels = data
        outputs = model(inputs)
        loss = loss_function(outputs, labels)
        total_loss += loss.item()/len(data)
        predicted = (outputs>0.5).float()
        truth = (labels>0.5).float()
        correct += (predicted == truth).float().sum()
  
    accuracy = correct/data_size
    total_loss = total_loss/data_size
print(f'Total Loss: {total_loss}')
print(f'Accuracy: {accuracy}')

Total Loss: 0.00034371729259089455
Accuracy: 0.8561246395111084

El resultado de testing es de 85.6% de accuracy. Lo que es bastante bueno pero aún inferior que otros benchmarks donde por ejemplo registraron 88.16% de accuracy.

Visualización de embeddings

T-SNE

Una buena forma de entender la capacidad informativa de nuestros embeddings es visualizándolo. Sin embargo, considerando que los seres humanos solo podemos ver en 3d y considerando que nuestro modelo contiene embeddings con dimensionalidad superior a tal numero, debemos aplicar algún tipo de técnica que pueda representar la data en una menor dimensionalidad (por lo general 2d). Así, una de las técnicas más conocidas para este fin es T-SNE, sólo desarrollado hace algunos años. El cual implementaremos a continuación de extraer los embeddings en un formato más cómoda para su visualización.

w = list(model.parameters())
embed_dict = {col: (categ_cols_mapping[col][0], w[i].detach().numpy()) for i, col in enumerate(categ_cols)}

def plot_embed(embed_dict, col, perplexity = 2, n = 2 ):
    """
    Función que genera una visualización en menor dimensionalidad de un embedding
    Input:
    embed_dict (diccionario): Diccionario de embeddings
    col (string): Nombre de variable categórica
    perplexity (float): Parámetro utilizado por el TSNE para calcular la 
    representación.
    n (int): Dimensionalidad de la representación resultante de TSNE.
    """
    # Primero instanciamos TSNE
    tsne = TSNE(n_components = n, init='pca', random_state=43, 
          method='exact', perplexity=perplexity)
    # Ajustamos a nuestro embedding original obteniendo la representacion TSNE.
    X_embed = tsne.fit_transform(embed_dict[col][1])

    # Creamos un objeto para visualizar la representación TSNE.
    fig, ax = plt.subplots(nrows = 1, ncols = 1, figsize = (5, 5))
    # Graficamos la representación (data)
    ax.scatter(X_embed[:,0], X_embed[:,1])
    ax.set_title('TSNE - ' + col) # titulo

    # Etiquetamos cada punto para mayor claridad
    texts = [ax.text(X_embed[i,0], X_embed[i,1], txt) for i, 
       txt in enumerate(embed_dict[col][0])]

    # Utilizamos la función adjust_text para mejor distinción de cada etiqueta
    adjust_text(texts)

Para visualizar el efecto de embeddings, seleccionamos una variable especialmente ilustrativa: marital-status o estado marital. La cual, describimos las categorías de acuerdo a la referencia original de repositorio de la UCI – Machine Learning.

Divorced: Divorciado
Married-AF-spouse: Casado(a), con esposo (a) de fuerzas armadas
Married-civ-spouse:Casado(a), con esposo (a) civil.
Married-spouse-absent: Casado(a), con esposo (a) ausente
Never-married: Nunca casado
Separated: Separado
Widowed: Viudo

plot_embed(embed_dict = embed_dict, col= 'marital-status',  perplexity = 2)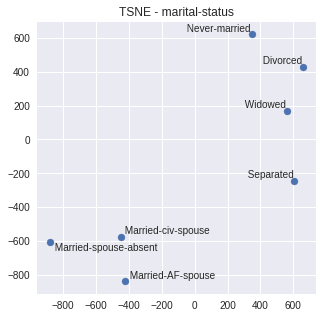

png

A partir de la visualización no es difícil notar dos clusters salientes: individuos actualmente casados vs actualmente no casados. Incluso es posible distinguir que el cluster de casados al parecer es más cohesionados que los no casados. Este tipo de análisis es una de las ventajas de utilizar embeddings: No solo podemos reducir dimensionalidad para esta variable, también, casi gratuitamente, nos entrega conocimiento que antes no teníamos. Esto, como veremos más adelante es útil para este modelo como para otros tipos de problemas.

Comparación con XGBoostClassifier

Nuestra previa comparación de la red neuronal, sugirió que nuestro modelo se desempeñó bastante bien pero no lo suficiente para vencer al benchmark referido. Sin embargo, para analizar un poco más en detalle el desempeño del modelo, realicemos una evaluación interna. En específico comparemos, utilizando los mismos datos, nuestro modelo versus un modelo importado desde una librería muy popular dentro de los participantes de kaggle: XGBoost. La cual es una librería que implementa modelos del tipo gradient boosted trees, que por lo general se desempeñan bastante bien, gracias a la flexibilidad y capacidad de generalización que ofrecen.

XGBoostClassifier sin Embeddings

El primer escenario es ajustar la data sin embeddings. Es decir utilizando one- hot encoding para la variables categóricas.

xgbmodel = xgb.XGBClassifier(n_estimators=400, seed = 43)
xgbmodel.fit(train_x_onehot, train_y)
xgbmodel.score(test_x_onehot, test_y)

0.8708768440245317

Vemos que obtenemos un accuracy de 87.08%. Un tanto mejor que nuestro accuracy de testing de nuestra red neuronal.

XGBoostClassifier + embedding

Sin embargo, el hecho que nuestra red haya obtenido un peor accuracy no significa que tengamos que desecharla. De hecho, lo que podemos hacer es combinar ambas. Para ello, tomaremos el mismo dataset de entrenamiento y testing que utilizamos para xgboost, pero donde reemplazaremos las columnas categóricas codificadas como one-hot enconding con los embeddings que encontramos mediante nuestra red neuronal.

def onehot_2_embed(df, cols, embed_dict):
    """
    Agrega las columnas de embeddings al dataframe original (df)
    generando un nuevo dataframe.
    Input:
    df (Dataframe): DataFrame que contiene variables categoricas y cóntinuas.
    cols (Lista): Lista de columnas cátegoricas a convertir
    embed_dict (Diccionario): Diccionario que almacena los embeddings.
    """

    copied = df.copy() # creamos una copia del df
  
    for col in cols: #iteramos cada var categórica
        embed_range = range(0, embed_dict[col][1].shape[1])
        onehot_len = embed_dict[col][1].shape[0]
        onehot_range = range(0, onehot_len)
        # creamos la lista de nombres de columnas de embeddings
        embed_cols = [col+ '_embed_' +str(j) for j in embed_range]
        # Conctenamos nuestra copia del df con columna de embeddings vacías
        copied = pd.concat([copied, pd.DataFrame(columns=embed_cols)])

        # Creamos listado de columnas one_hot encoding
        onehot_cols = [col + '_onehot_' + str(i) for i in onehot_range]
        # Guardamos el nombre de la primera columna de onehot
        first_onehot_col = col + '_onehot_0'

        # En nuestro nuevo dataframe creamos esa primera columna que no habíamos 
        # generado anteriormente con get_dummis (skip_first = True)
        copied[first_onehot_col] = 0.0

        # buscamos los índices cuando todas las columnas onehot salvo la primera 
        # sean 0
        all_zero_indexes = copied[copied[onehot_cols].nunique(axis = 1).eq(1) == True].index
        # Ahora para solo la primera columna, y para cuando todo el resto de otras 
        # columnas sean 0, cambiamos el valor de esas filas por 1.0
        # Es decir revertimos el efecto de cuando codificamos con one hot encoding
        # donde no consideramos la primera columna.
        copied.loc[all_zero_indexes, first_onehot_col] = 1.0

        # finalmente iteramos por cada categoría
        for i in onehot_range:
            # especificamos el nombre de cada columna onehot.
            onehot_col = col + '_onehot_' + str(i)
            # y obtenemos los indices de filas para cuando esa categoría es 1.
            indexes = copied.loc[copied[onehot_col]==1, :].index

            # luego completamos con los valores respectivos de embeddings para las 
            #columnas de embeddings  respectivas para esas filas.
            copied.loc[indexes, embed_cols] = embed_dict[col][1][i]

            # finalmente convertimos a float64, como lo pide xgboost
            copied[embed_cols] = copied[embed_cols].astype('float64')
    return copied

Generamos nuestra nueva data de entrenamiento agregando las columnas de embeddings salvo la columna sex.

train_x_copied = onehot_2_embed(train_x_onehot, categ_cols[:-1], embed_dict)

Eliminamos las columnas del tipo one_hot encoding.

train_x_copied = train_x_copied.loc[:, ~train_x_copied.columns.str.contains('onehot')]

Lo mismo hacemos para nuestro dataset de validación.

test_x_copied = onehot_2_embed(test_x_onehot, categ_cols[:-1], embed_dict)
test_x_copied = test_x_copied.loc[:, ~test_x_copied.columns.str.contains('onehot')]

Training

xgbmodel = xgb.XGBClassifier(n_estimators=400, seed = 43)
xgbmodel.fit(train_x_copied, train_y)
xgbmodel.score(test_x_copied, test_y)

0.8740261892922261

Analizando el resultado, vemos una mejoría. Pasamos de 87.08% a 87.4%. Es decir, más de 3 décimas. A pesar que este incremento, para muchos, puede parecer despreciable, no debe ser considerado como tal. Por ejemplo, en Kaggle, un entorno muy competitivo estas pequeñas mejoras pueden marcar la diferencia entre los ganadores de la competencia y los que no.

Además de ello, debemos notar un punto importante. Que la técnica de tomar los embeddings entrenadas con un modelo para utilizarla en otro modelo, no se debe restringir solamente a este dataset. De hecho, la estrategia de reutilizar embeddings para distintos dataset se utiliza mucho para entrenar modelos de lenguaje natural. Es tan así, que existen embeddings conocidos para inglés como el mismo word2vec o Glove, que son fácilmente descargables y aplicables a cada problema de lenguaje natural de forma más personalizada.

En Resumen…

Hay varios puntos a sacar en limpio. Primero, mostramos que un modelo de red neuronal puede ser competitivo para datasets tabulares, en comparación con modelos más comúnmente utilizados como XGBoostClassifier. Segundo, que embeddings no solo es aplicable a variables de texto – de hecho es una técnica muy flexible, desarrollandose investigación en, por ejemplo: embeddings de imágenes, oraciones, sonidos y más – también es fácilmente traspasable a variables categóricas. Finalmente, y más importante creo, mostramos paso a paso cómo generar embeddings con Pytorch y describiendo el valor que esta técnica entrega. En específico, la implementación de embeddings nos permitió reducir dimensionalidad y de paso capturar información. De hecho, mostramos que los embeddings los podemos utilizar para otros fines, como clusterización de variables categóricas o para mejorar el desempeño de otros modelos.